引言:
生成式建模的扩散思想实际上已经在2015年(Sohl-Dickstein等人)提出,然而,直到2019年斯坦福大学(Song等人)、2020年Google Brain(Ho等人)才改进了这个方法,从此引发了生成式模型的新潮流。本文将基于论文Denoising Diffusion Probabilistic Models,解读扩散模型的过程和原理。
扩散模型包括前向加燥过程以及反向去噪过程,简单来说前向加燥过程就是在每一个时间步上往样本里 增加高斯噪声,直到样本失去区分性;而反向去噪过程就是通过在每一个时间步上进行去噪来重建图像。
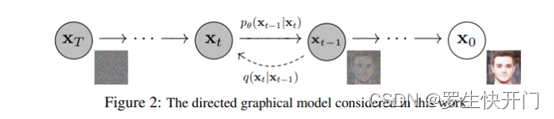
给定真实图片样本式,diffusion前向过程通过T次累计对其添加高斯噪声,得到:
β用于控制噪声的权重,原文中随着时间步数逐渐增大。x和ε系数的平方和恒等于1满足勾股定理,可以看作直径为1的半圆中内接直角三角形的两条边的长度,β和1-β可以看作两条直角边相邻正方形的面积。
从公式中我们可以看出从x0到xT需要一个递归的过程,如果进行递归计算的话,在T值比较大的情况下,计算过程是比较慢的,那么可不可以进行一次计算直接从x0得到xt呢?
我们把xt-1与xt-2的关系式代入到xt与xt-2的关系式中得到(在后续的计算中,α=1-β):
其中每次加入的噪声都服从高斯分布z1,z2,⋯,~N(0,1)。
因此,将上面的式子展开:
括号中的两项分别服从
相加之后的结果服从
化简之后的公式就可以写成:
最终,经过递推得到:
其中为
,只需要知道时间步t的值以及原始
的分布,就可以得到
的分布。
2.反向去噪过程
反向去噪过程就是根据已知的xt去求得原样本x0的分布。
根据贝叶斯公式,我们可以了解到:
根据上面加噪过程的推理,我们已知:
因此:

继续展开,得到:

根据标准正态分布的展开:

可以得到方差和均值,其中均值为:

由于反向推倒过程中,x0是未知的,但是x0可以由xt表示:
最终得到:
从以上推导可以知道,根据xt我们可以求出xt-1的方差和均值。但均值中的噪声zt是未知的,因此我们需要使用模型去估计zt。估计出噪声之后我们就可以根据噪声zt计算出xt-1的均值和方差,得到p(xt-1|xt,x0)的概率分布。
以下是原文中给出的伪代码,左边是训练噪声估计模型的过程,右边是去噪采样过程。

参考文献:
https://arxiv.org/abs/2006.11239
【stable diffusion】3小时终于搞懂了Diffusion模型数学原理及源码复现!扩散模型、diffusion model_哔哩哔哩_bilibili
【深度学习模型】扩散模型(Diffusion Model)基本原理及代码讲解-CSDN博客

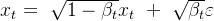

oivv7e